Probabilistic Model
P(“I saw a van”) = P(“I”) x P(“saw” | “I”) x P(“a” | “I saw”) x P(“van” | “I saw a”)
This is not possible because the size of a sentence is unbounded.
Smaller Limit: N-Gram
Probability of next word only depends on the previous N-1 words.
Unigram: Bigram:
If a single n-gram in the sentence has never been seen, P=0, the entire probability becomes 0. One unusual word can make a sentence from “likely” to “impossible”.
Solution: we can remove 0s - Laplace Smoothing
- start each count at 1
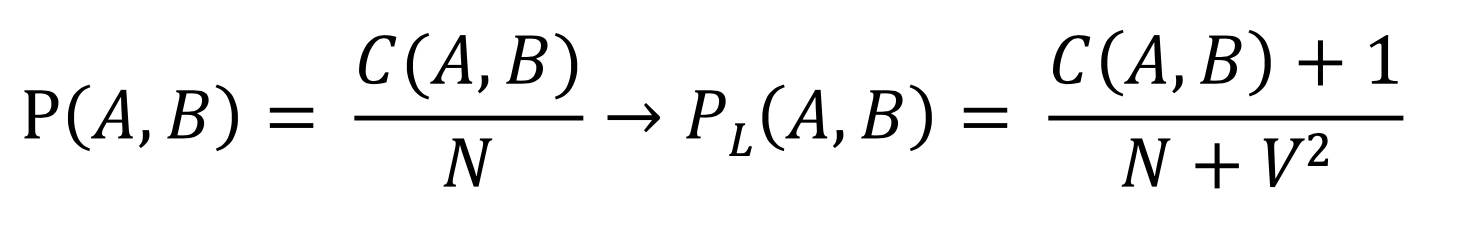+ because every pair of words has a +1, V = vocabulary size
Other Smoothing Techniques
- Good-Turing
- Katz backoff
- Jelinek Mercer
- Dirichlet Smoothing
- Kneser-Ney
Searching - Information Retrieval
Inverted Index
Map context to documents
Ex:
blue -> 2
cat -> 3
fish -> 1 -> 2
Key is word, value is index of the document they appear in
Zipf’s Law
- A few elements occur very frequently
- Many elements occur very infrequently
Delta Compression
- if a term is rare => not many postings
- if a term is common => average delta is small
Hence we can use delta encoding (gap encoding)
Ex:
1, 6, 11, 15, 22 // sequence
1, 5, 5, 4, 7 // gaps
This saves space because we can use other datatypes (not int)
VInt (variable-width integer type) uses 1-5 bytes to represent an int.
Also, use BytesWritable instead of ArraysWritable[VInt] because array storing is heavy.
WORD Level: Simple 9 - Simple 14 (different ways of storing a variable number of values in a single word) BYTE Level: VInt - VLong BIT Level: Elias Code
Elias Gamma Code
Assumptions:
- Natural numbers with no upper bound
- Small numbers are more common than large numbers
- Values are distributed by a power law
Golomb Code
Each term gets its own custom encoding scheme.
For situations where we only care about contains or not contains and not the number of times a term appears in a document.
Retrieval
Boolean Retrieval
Query is formed using boolean operators (AND OR NOT)
Term at a time
For each term, generate sets of documents => only holds 2 sets in memory at a time.
Document at a time
Check if document passes the query. Since the documents are in sorted order, modify merge operation.
Ranked Retrieval
Requires relevance function => sort by relevance
One way to be relevant
- terms that occur many times in one document should have high weights
- terms that occur many times in the entire collection should have low weights
We need:
- term frequency (in document)
- document frequency (number of documents)
TF-IDF (Term Frequency and Inverse Document Frequency)
Document at a time
For each document:
- score each query term, and add them all up
- accumulate best k hits (min-heap)
Pros: time is O(nlogk) space is O(k) Cons: cannot terminate early
Term at a time
- Collect hits and ranking for rarest term into accumulator
- for each other term in the query:
- if a document does not have that term - remove from accumulator
- otherwise, add next term’s ranking to overall ranking
Pros: can terminate early Cons: uses a lot of memory